Вспомнил детство. А как извлечь корень квадратный врукопашную?

Первый способ – разложение подкоренного выражения на множители.

Например, найдем 

Число  делится на 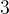 (так как сумма его цифр делится на 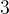). Разложим  на множители:

Найдем . Это число делится на . На 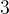 оно тоже делится. Раскладываем  на множители.

Еще пример.

Есть и второй способ. Он удобен, если число, из которого надо извлечь корень, никак не получается разложить на множители.

Например, надо найти . Число под корнем – нечетное, оно не делится на 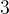, не делится на 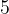, не делится на … Можно и дальше искать, на что же оно все-таки делится, а можно поступить проще – найти этот корень подбором.

Очевидно, что в квадрат возводили двузначное число, которое находится между числами  и , поскольку , , а число  находится между ними. Первую цифру в ответе мы уже знаем, это .

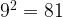Последняя цифра в числе  равна . Поскольку ,   , последняя цифра в ответе – либо , либо . Проверим:

. Получилось!

Найдем .

,   . Значит, первая цифра в ответе – пятерка.

В числе  последняя цифра – девятка. 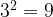,   . Значит, последняя цифра в ответе – либо 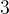, либо .

Проверим:

Если число, из которого надо извлечь квадратный корень, заканчивается на  или  – значит, квадратный корень из него будет числом иррациональным. Потому что ни один квадрат целого числа не заканчивается на  или . 

Источник: ege-study.ru

Я, правда пользовался вот этим способом:

Вот такое у меня было детство - без калькуляторов, со счетами, логарифмической линейкой и письменными принадлежностями.